I just scheduled my final exam for my discrete mathematics course, now that I submitted my homework for the final assignment covering graph theory. Throughout this assignment, I was introduced to a variety of concepts: Leonard Euler and his discovery of Euler paths and circuits, Hamiltonian paths and circuits, and a handful of graph related terminology (e.g. vertex, edges, degrees, bridge, cut-vertices, isomorphic graphs, trees, forests).
In addition to the concepts above, I learned two different ways to represent graphs in (computer) memory. One approach is using adjacency matrix, a matrix whose columns and rows are represented by each vertex. The second way to represent a graph is by an incidence matrix; unlike an adjacency graph, an incidence matrix’s columns are vertices, the rows representing edges.

Although the lesson only scratched the surface on graph theory, I reveled in the fact that many of the terms I learned were actually terms that I encountered at work, terms that I had no idea were rooted in mathematics.
For example, the term forest (in graph theory) is defined as a collection of trees; I encountered this term while working as a system administrator, a time when I managed Active Directory (a centralized authentication system) and all the security rules and policies bound to a forest.
In addition to the example above, I find comfort in the fact that some data structures (e.g. binary search tree) and algorithms (e.g. breadth first search) that I’ve studied in the past build on top of graph theory.
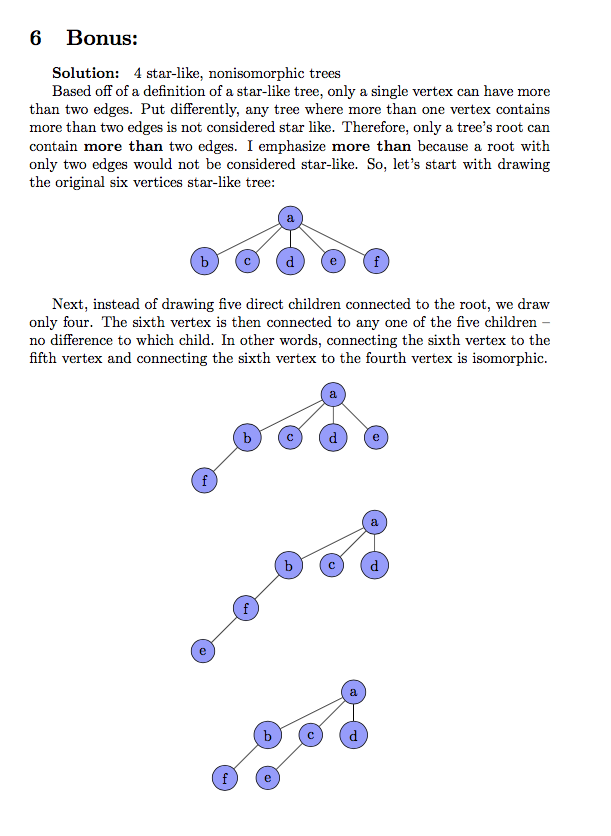
In any case, I really enjoyed learning about graph theory, a lesson I’ll continue to build on top of as I pursue my life long study of mathematics and computer science.